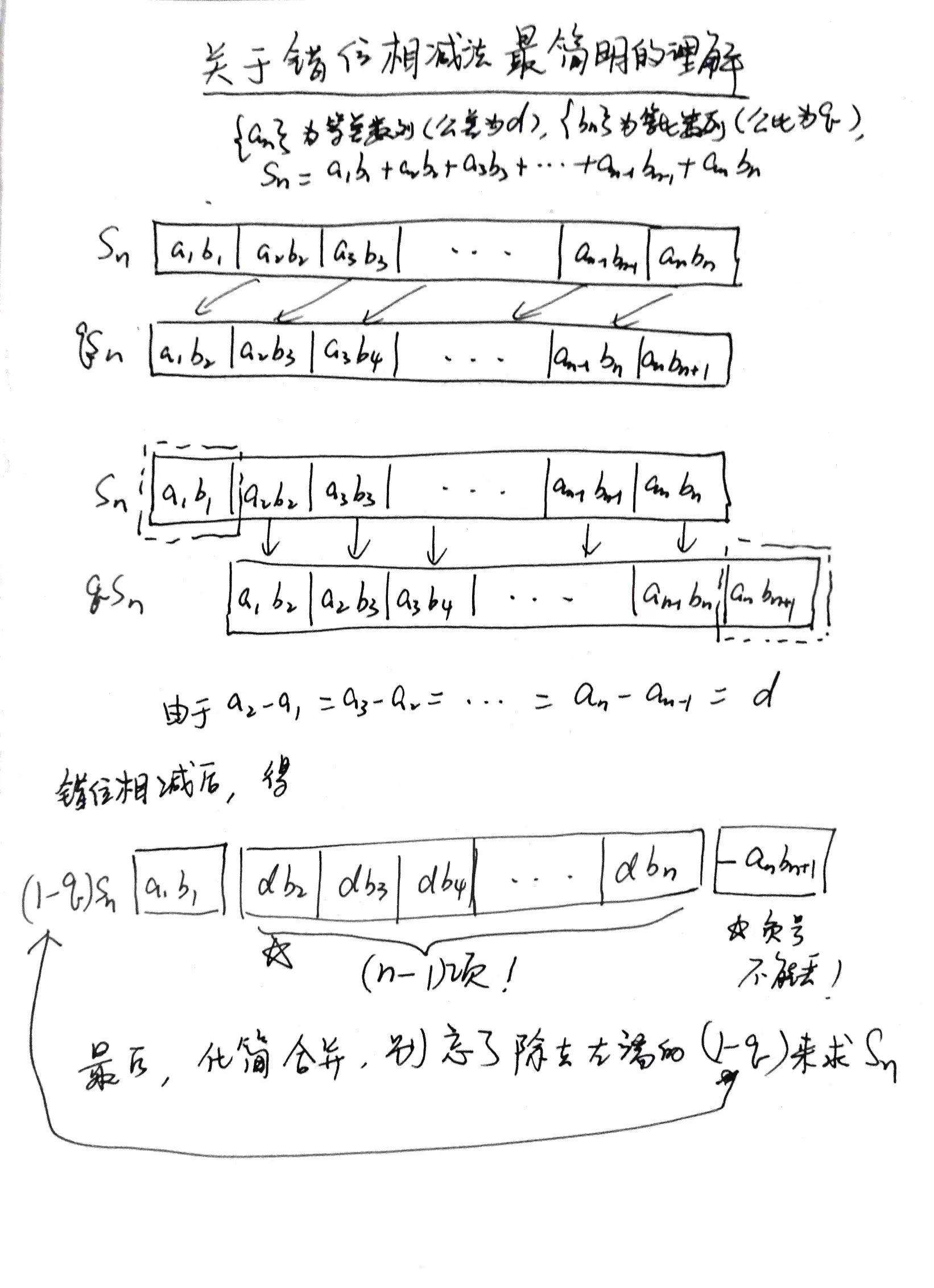
高中数学有一类常见问题：数列{an}为等差数列，数列{bn}为等比数列，令cn=an·bn，要求数列{cn}的前n项和Sn.
通常，老师会讲用错位相减法来做（错位相减法在等比数列求和公式推导时已经学过），过程如下：
而如果用我们现在要讲的解法：
这么简单？！
那这种方法是只适用于这道题目呢，还是对等差乘等比数列求和这类问题都可以用？
我们仔细来看下构造这一步的详细过程。
相信你已经看明白了，只要{an}是等差数列，就一定可以像图中一样用待定系数法进行构造，使cn变成一个新数列{dn}的相邻两项之差。
对于上面这个例题，dn=(n-1)3^n，
n≥2时，cn=dn-d(n-1)，
c1=1，c2=d2-d1，c3=d3-d2，……
那对cn求和就相当于裂项相消了：
Sn=c1+c2+c3+……+cn
=1+d2-d1+d3-d2+……+dn-d(n-1)
=1-d1+dn=1-0+(n-1)3^n=(n-1)3^n+1.
为了讲解清晰，我们把运算过程完全展开了，实际上步骤并不复杂。
相比错位相减法，我认为这个方法是有优势的，你掌握了吗？
派优网部分新闻资讯、展示的图片素材等内容均为用户自发上传(部分报媒/平媒内容转载自网络合作媒体)，仅供学习交流。用户通过本站上传、发布任何内容的知识产权归属用户或原始著作权人所有。如有侵犯您的版权，请联系我们一经核实，立即删除。并对发布账号进行封禁。
